동국대학교 수학교육과 > 교과과정 > 수학교육과 교과 과정

popup zone

등록된 팝업이 없습니다

수학교육과 교과 과정

교육목표

수학교육의 목표는 대한민국 교육 이념에 부응하는 능력 있는 수학교사를 양성하는데 있다. 구체적으로 수학 교수·학습에대한 목표는 중·고등학생들에게 자기 자신과 지역사회 및 국가 그리고 인류사회 발전에 필요한 수학의 학문적 이론과 응용력을 겸비할 수 있도록 지도할 수 있는 교사를 양성하는데 있다. 이것을 만족시킬 수 있는 구체적인 요소는 수학과 교육과정의 숙지 및 창의적 개발 능력, 효과적이고 다양한 수학교육방법의 수행 능력 및 응용 능력, 효율적인 수학 교육 보조 자료의 활용 능력, 그리고 교수·학습과 연계된 적절한 평가 방법에 관한 이론적 연구 및 실행 능력과 교육 심리학적 전문가로서 학생 지도에 실질적이고 유용한 이론을 체계적으로 학습하고, 교육자로서의 지도적인 인격을 도야하고 함양할 수 있도록 하여 환경을 조성하여 유능한 중등교사가 될 수 있도록 한다.

졸업 후 진로

수학교육과를 졸업하면 중ㆍ고등학교 교사와 학원 강사, 교수, 수학교육과 관련된 연구원, 금융보험업 등 다양한 분야로 진출할 수 있다.

최저이수학점 기준표

가. 신입학생

구분/입학년도			2008	2009~2012	2013	2014~2015	2016~2018	2019	2020
교양	공통교양 (기초교양)		12~14	12~16	12	25~29	31	31	31
	핵심교양		12	12	12	–	–	–	–
	학문기초 (외국어영역 또는 자연과학영역)		6~8	6~8	6~8	6~8	6~8	6~8	6~8
전공	단일전공 이수자		54	54	54	54	54	54	54
	복수전공 이수자	주전공	42	50	50	50	50	50	50
		복수전공 (사범대)	42	50	50	50	50	50	50
		복수전공 (비사범대)	복수전공 대학(학과)의 학점 기준에 따름
교직	교직이론		14	14	12	12	12	12	12
	교직소양		–	4	6	6	6	6	6
	교육실습		2	4	4	4	4	4	4
졸업요건	취득학점		130	130	130	130	130	130	130
	평점평균		2.0	2.31	전공: 2.31 이상 / 교직: 2.75 이상
	외국어시험(TOEIC)		680	700	700	700	700	700	700
	영어강의
	교직적성및인성검사		1회 이상 적격		2회 이상 적격
	응급처치및심폐소생술		2회 이상 이수
	졸업논문		졸업시험으로 진행

나. 편입학생

구분/편입학년도			2008~2014	2015~2016	2018	2019	2020
교양	공통교양 (기초교양)		2~4	2~4	2~4	2~4	2~4
	학문기초 일반교양	2학년편입	32	32	32	32	32
	학문기초 일반교양	3학년편입	0(6~8)	0(6~8)	0(6~8)	0(6~8)	0(6~8)

교직과정 이수

1. 무시험검정 합격 기준

구 분	2013학년도 이후 입학자부터
전공과목	◦ 50학점 이상 – 기본이수과목 21학점(7과목) 이상 포함 – 교과교육영역 8학점(3과목) 이상 포함
교직과목	◦ 22학점 이상 – 교직이론 12학점(6과목) 이상 – 교직소양 6학점(3과목) 이상 – 교육실습 4학점 이상
성적기준	◦ 전공과목 평균성적 75/100점 이상 ◦ 교직과목 평균성적 80/100점 이상
기타	◦ 교직 적ㆍ인성검사 적격판정 2회 이상 ◦ 응급처치 및 심폐소생술 실습 2회 이상 ◦ 산업체 현장실습 이수확인서(공업계 표시과목 취득자) ◦ 기타 대학의 장이 별도로 정하는 기준

○ 입학년도에 대한 해석
가. 사범대학 학생: 신입학한 학년
나. 교직설치학과 교직이수자: 교직과정 선발년도-1(2학년에 선발)
ex) 수학과 2010학년도 입학자가 휴학 후 복학하여 2015학년도에 교직과정 이수자로 선발
될 경우 교직이수 요건에 따른 입학년도는 2014학년도(2015-1)로 적용
다. 교직복수(연계)전공 이수자: 주전공 입학년도에 따른 검정기준을 적용
2. 전공과목 이수 기준

가. 이수 학점 기준
– 사범대학 재학생 : 54학점 이수(전공(전문) 50% 이상 이수)
– 비사범계 교직과정 이수자

학과별 졸업 전공학점 이수 기준5 〉학점 = 학과별 졸업 전공학점 이수 기준 이수
학과별 졸업 전공학점 이수 기준 〈 50학점 = 50학점 이수

나. 기본이수과목
학과(전공)별로 지정된 기본이수과목 7과목 21학점 이상 이수
– 기본이수과목은 전공학점에 포함되나, 지정된 기본이수과목이 타 학과(전공) 개설 전공과목 또는 교양과목인 경우 기본이수과목으로는 인정되지만 전공최저이수학점에는 포함되지 않음에 유의
※ 반드시 학과(전공)별 지정된 기본이수과목(13페이지)을 이수하여야 함(유사과목 대체이수 불가)

다. 교과교육영역
학과(전공)별로 지정된 교과교육영역 3과목 9학점 이상 이수
– (표시과목별)교과교육론, (표시과목별)교과교재연구 및 지도법, 교직 논리 및 논술

교직과목 이수 기준

영 역	학수번호	교과목명	이수구분	학점	비고
교직이론	ERC0001	교육학개론	직필	2	교직이론 과목 중 6개 과목(12학점) 이상 선택 이수
	ERC0002	교육심리	직필	2
	ERC0003	교육철학 및 교육사	직필	2
	ERC0005	교육사회	직필	2
	ERC0006	교육방법 및 교육공학	직필	2
	ERC0007	교육행정 및 교육경영	직필	2
	ERC0018	생활지도 및 상담	직필	2
	ERC0011	교육과정	직필	2
	ERC0012	교육평가	직필	2
교직소양	ERC0013	교직실무	직필	2	3개 과목 필수 이수
	ERC0019	특수교육학개론	직필	2
	ERC0020	학교폭력예방 및 학생의 이해	직필	2
교육실습	ERC0021	학교현장실습	직필	2	3개 과목 필수 이수 (세부 이수방법 참조)
	ERC0022	교육봉사활동1	직필	1
	ERC0023	교육봉사활동2	직필	1

교직이론과목(6과목 선택이수)				대체이수과목
이수구분	학수번호	교과목명	학점	이수구분	학수번호	교과목명	학점
직필 (교직이론)	ERC0001	교육학개론	2	전공 (교육학과)	EDU2013	교육학개론	3
	ERC0002	교육심리	2		EDU2015	교육심리	3
	ERC0003	교육철학 및 교육사	2		EDU2002	교육철학	3
	ERC0005	교육사회	2		EDU2010	교육사회학	3
	ERC0006	교육방법 및 교육공학	2		EDU4003	교육공학	3
	ERC0007	교육행정 및 교육경영	2		EDU2016	교육행정	3
	ERC0018	생활지도 및 상담	2
	ERC0011	교육과정	2		EDU2014	교육과정	3
	ERC0012	교육평가	2		EDU4035	교육평가	3

성적 및 기타 기준

가. 성적기준

– 전공과목 평균성적 75/100점 이상 → 2.31/4.5 이상
– 교직과목 평균성적 80/100점 이상 → 2.75/4.5 이상나. 교직 적성 및 인성검사

·이수 대상별 적격 판정 횟수

신입학	편입학	판정 횟수
2013학년도 이후 교원양성과정 이수자	2015학년도 이후 교원양성과정 이수자	졸업 전까지 적격 판정 2회 이상
2012학년도 이전 교원양성과정 이수자	2014학년도 이전 교원양성과정 이수자	졸업 전까지 적격 판정 1회 이상

·이수 대상별 지정된 학기에 의무 실시를 원칙(적격 판정 2회 이상 학생 기준)

구 분	교원양성과정 이수 대상
구 분	사범대학	교직과정
1학년 1학기(1학기)	1차 검사
1학년 2학기(2학기)
2학년 1학기(3학기)
2학년 2학기(4학기)
3학년 1학기(5학기)		1차 검사
3학년 2학기(6학기)
4학년 1학기(7학기)	2차 검사	2차 검사
4학년 2학기(8학기)

– 휴ㆍ복학 등 부득이한 사정으로 지정된 학기에 미 실시할 경우 다음 학기에 실시 가능
• 단, 최소 1년 간격을 준수하지 않아 추후 발생하는 문제에 대해서는 학생 개인에게 책임이 있음.
ex) 교육부감사로 인한 교원자격증 발급 취소 등(졸업 후에도 발급 취소 및 자격박탈 가능성 있음) • 교직 적성 및 인성 검사 1회 이상 적격 판정 시 학교현장실습 이수가능

나. 교직 적성 및 인성검사 방법

– 매 학기중(4월, 10월) 홈페이지 공지사항의 적성 및 인성검사 기간 및 방법을 확인 후 실시
• 검사 방법 : nDRIMS를 통한 학생 개별 온라인 검사
• 검사 적격판정 : 검사 실시 후 2주 이내에 nDRIMS를 통한 학생 개별 확인 가능
※ 부적격 판정자의 경우 별도의 프로그램 실시

– 검사 진행 세부 절차

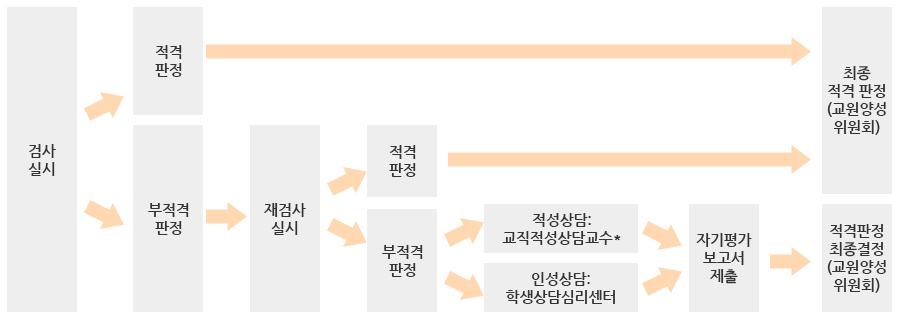
검사 진행 세부 절차

* 교직적성상담교수 : 전공지도교수(사범대학 재학생), 교직부장(비사범계 교직과정 이수자)

다. 응급처치 및 심폐소생술 실습

＊대상 : 교원양성과정을 이수중인 재학생 및 수료생(사범대학, 교육대학원, 교직과정)
＊시기 및 횟수

▪ 교원양성과정 이수 기간 중 총 2회 이상 실시
– 사범대학 재학생 : 입학시점 ~ 졸업시까지
– 비사범계 교직과정 이수자 : 교직 선발시점 ~ 졸업 시까지
※ 수료생의 경우 수료일자에 따라 의무횟수 달리 적용

수료일자	2016.02 이전	2016.08	2017.02 이후	비고
의무횟수	0회	1회	2회	규정시행일 16.03.01

▪ 이수 대상별 지정된 학기에 의무 이수를 원칙

구 분	교원양성과정 이수 대상
구 분	사범대학	교직과정
1학년 1학기(1학기)	이수
1학년 2학기(2학기)
2학년 1학기(3학기)
2학년 2학기(4학기)
3학년 1학기(5학기)	이수	이수
3학년 2학기(6학기)
4학년 1학기(7학기)		이수
4학년 2학기(8학기)

※ 대한심폐소생협회의 응급처치 및 심폐소생술 교육 유효기간(2년)을 고려하여 대상별 간격 조정 ▪ 휴ㆍ복학 등 부득이한 사정으로 지정된 학기에 미 실시할 경우 다른 학기에 이수 가능. 단, 실습 횟수의 인정은 학년도별 1회임.

＊응급처치 및 심폐소생술 실습 이수 방법
– 매 학기중 홈페이지 공지사항을 확인 후, 실습 실시(매 학기 과정 개설)

응급처치 및 심폐소생술 실습 이수 방법

라. 산업체 현장실습

＊ 대상 과목 : 공업계 표시과목(전자전기공학부 : 전기ㆍ전자ㆍ통신, 화공생물공학과: 화공ㆍ섬유)
※ 주전공 또는 복수전공으로 위 과목의 교사자격을 취득하고자 하는 경우 산업체 현장실습 이수 필수
* 현장실습 기간 : 4주
* 이수방법 및 절차
① 공과대학에서 주관(청년기업가센터와 연계)하는 「현장실습」과목 이수
② 현장실습 과목 이수 후 다음 학기 「산업체 현장실습」 수강신청
③ 현장실습 결과보고서 교직부 제출
④ 현장실습 결과보고서 및 평가서를 바탕으로 교직부에서 산업체 현장실습 성적처리
※ 산업체 현장실습(ERC0010)은 0학점 P/F제로 운영
* 현장실습 과목 이수 관련 문의 : 공과대학 교학팀 02-2260-3862
* 2018학년도 이후 공과대학 교직선발 폐지

교과목해설

MAE2001	대수 및 기하	Algebra & Geometry
복소수, 정식의 성질, 대수 방정식의 근, 벡터 행렬에 관한 기초지식을 배워 해석학, 대수학, 기하분야로의 입문에 교량적인 역할을 하게 한다.
This course deals with the basic properties of a complex number, a polynomial, a equation, a vecter, a matrix and a linear transformation
MAE2002	논리와 집합	Set Theory
명제의 기본형식을 도입하고 집합의 개념, 포함관계와 그 연산을 다루고 집합의 대등한 관계를 정의함으로서 유한집합과 무한집합의 성질과 기수의 개념과 기수의 부등식, 그리고 기수의 덧셈과 곱셈 및 기수의 지수법칙과 연속체의 가설을 배운다. 선택공리로 시작하여 극대원리, Zorn의 보조정리 초한 귀납법을 다룬다.
This course is designed to introduce the basic format of propositions, deals with the concept, inclusion relations and operation of a set, and defines the equal relation of a set, which leads to learning the characteristics of a finite set and a infinite set, the inequality of cardinal numbers, addition and multiplication of cardinal numbers, the exponential law of cardinal numbers and the hypothesis of continuum. Starting from the axiom of choice, maximization principle and the lemma of Zorn and transfinite induction are studied in this course.
MAE2017	응용수학방법론	Methods of Applied Mathematics
응용수학의 토픽을 다루는 교과목으로 자연과학과 공학, 사회과학에서 나타나는 여러 가지 수학의 응용을 배운다. 미분적분학, 선형대수학, 해석학을 이수한 것을 전제로 여러 가지 미분방정식과 각 분야의 응용수학 모델을 공부한다.
This course is to deal with applied mathematics topics which appear in natural science, engineering and social science. When having completed the required courses, calculus, linear algebra and analysis, we will acquire the basic theory of differential equations and study applied mathematical models in various fields.
MAE2021	수학교육과정	Mathematics Curriculum
제7차 및 2007 개정 교육과정에 따른 중·고등학교 전체 수학교과서 내용의 전반적인 이해와 문제점 분석 그리고 그에 대한 적절한 교수법을 생각해 본다. 한국 수학교육과정과 외국수학교육과정을 비교 분석해 보고 NCTM Standards에서 제시한 수학교육과정 규준을 이해한다.
This course understands the contents of general math texts of middle / high schools according to 7th and 2007 revised curriculum, analyzes the problems and considers proper teaching methods for this. And this course also analyzes by making a comparison between Korean math curriculum and foreign math curriculum, and it understands math curriculum criterion that is presented by NCTM Standards.
MAE2022	해석학 1	Analysis I
중등학교의 수학교사가 되기 위한 예비강좌의 하나이다. 미분적분학을 바탕으로, 집합의 성질, 수의 체계 분류, 실수의 성질, 극한 개념과 연속성에 대한 규명을 하여 해석학의 기초이론을 다진 후, 이들 내용과 중 ·고등학교 수학교과내용과의 연계성을 연구한다.
It is one of the required courses to be a math teacher of middle or high schools. Based on differential and integral calculus, this course inquires into the characteristics of a set, the classification of numeral system, the characteristics of a real number, the utmost limits and the continuity, which leads to strengthening the basic theory of analysis and studying on the contents of the subjects mentioned above in the context of the contents of middle or high school mathematics.
MAE2023	조합 및 그래프 이론	Combinatorics and Graph Theory
이 과목에서는 순열, 조합, 수와 집합의 분할, 그래프이론, 생성함수 등의 이산수학적 주제를 다루면서 수학적 발견술의 방법을 익혀 이산수학의 교수학적 효과와 의미를 이해한다.
The course deals with such themes of discrete mathematics as permutation, combination, partitions of numbers and sets, graph theory and generating functions, acquiring the method for problem-solving in mathematics and understanding the meaning of discrete mathematics and its didactical effect.
MAE2024	선형대수 1	Linear Algebra I
중등학교 수학교사를 위한 교육과정의 하나로 연립1차방정식을 행렬로 표현하는 것을 배운다. 가우스소거법, 행렬과 행렬연산, 역행렬을 학습한다. 연립방정식과 가역성에 관한 여러 가지 결과를 배운다. 행렬식, 2차원과 3차원공간의 벡터, 유클리드 벡터공간을 공부한다.
This course deals with systems of linear equations and matrices. In this course students learn determinants, vectors in 2-space and 3-space, Euclidean vector spaces, and real vector spaces.
MAE2025	해석학 2	Analysis II
해석학의 기초를 이수한 후, 이를 바탕으로 도함수이론, 적분이론, 여러 가지 상황에서의 극한과 수렴에 대한 제반 개념을 고찰하고, 이들과 고등학교 수학교과내용과 연계된 부분의 효율적인 교육방법을 연구한다.
After completing the base of analysis education, on the basis of that, this course considers derivative theory, integral calculus theory and general concepts of the utmost limits and convergence in various conditions, which leads to studying an efficient teaching method in conjunction with the contents of high school math textbooks.
MAE2026	선형대수2	Linear Algebra II
기저와 차원, 행렬의 행공간, 열공간과 영공간, 계수와 퇴화차수를 공부한다. 직교행렬, 기저변환, 고유값과 고유벡터, 대각화법, 직교대각화법을 학습한다. 선형변환과 행렬의 상사성을 배운다.
This course deals with inner product spaces, eigenvalues, and eigenvectors. In this course students learn diagonalization, orthogonal diagonalization, and linear transformations.
MAE2027	기하학일반	Geometry
종래의 학교수학은 우선 결론이 있으며 그것을 학습하고 증명하는 것이 중심이었다. 그것에 대하여 목공형 도구를 이용한 수학에서는 스스로 실험하며 도형을 움직여 나가는 과정에서 결과를 발견하고, 증명을 생각하여 간다. 이러한 “수학을 한다”는 장면을 조금이라도 만들어 나가기 위한 과정이다. 그러므로 다양한 소프트웨어를 활용하여 종래의 기하교육에서 다룰 수 없었던 도형 등의 전반적인 성질과 관계를 조사한다.
The conventional school mathematics already has a conclusion and most of what they do at school is to learn and verify it. In the field of mathematics using wooden models, they discover the consequence and verify the process using the devices. It is regarded as a process to show a scene, “Doing the Math” at least. Therefore, using various kinds of software, this course investigates the general characteristics and the relations of devices which haven’t been used in the present geometric education.
MAE4018	수학교육자료분석	Data Analysis in Mathematics Education
수학교육통계 자료의 분석과 통계실습을 위한 과목이다. 다루는 내용은 기초통계학, 응용통계학, 수학교육통계 자료분석을 위한 자료수집 및 분석 또 나아가서는 교육평가에 요하는 수학교육 방법론의 자료를 수집 및 분석한다.
This course is for the analysis of statistics and the practice of statistics in mathematics education. Its contents are about basic statistics, applied statistics and the collection and the analysis of mathematics education. Furthermore, this course collects and analyzes the data needed for the education evaluation.
MAE4021	수학교육세미나	Seminar in Mathematics Education
수학교육의 목적과 내용, 수학교육의 실제, 수학교육에 관한 연구방향, 수학교육의 세계적인 동향과 교육과정, 수학 학습-지도의 방법 등을 다룬다.
This course deals with the purpose and the contents of mathematics education, the present condition of mathematics education, the direction of mathematics education research, international trend, courses and teaching and studying methods for mathematics education.
MAE4025	수학기초론	Principles of Elementary Mathmatics
중ㆍ고등학교의 수학교육 방법의 효율화를 위한 수학의 역사적 사실을 수학교육학적 견지에서 재구성하여 연대별 주제별로 분석하고 연구하여 중ㆍ고등학교 교사가 갖추어야 할 기본 소양을 길러주고 더 나아가 새로운 수학교육 방법을 개발할 수 있는 능력을 길러 준다. 이론적 접근법인 교육과정의 발생학적 방법을 체계화해본다.
For the efficiency of the math teaching methods for middle or high school, the historic mathematics factors will be reorganized in terms of mathematics education, analyzed and studied according to the period of time and themes for middle or high school math teachers to have a basic grounding in the history of mathematics and have a capability to develop their own teaching skills. It is to give a concrete form to the theoretical approaching way, the embryologic methods of educational process.
MAE4030	수학교육사	History of Mathematics Education
고대수학, 중세수학, 인문주의 교육시대, 실재주의 교육발전, 18세기 및 19세기의 전반의 수학교육, 19세기 후반의 수학교육의 정체시대, 20세기의 수학교육사에 관하여 다룬다.
This course deals with the history of mathematics education, such as ancient math, medieval math, the math in the time of humanism, the math in the 18th century and the early 19th century, the math in the stagnation time in the late 19th century and the math in the 20th century.
MAE4031	수학적문제해결론	Mathematical Problem Solving
수학적인 사고의 육성, 수학적인 사고의 구체적인 내용의 명확화, 수학적인 사고를 기르는 지도법, 수학적 사고의 가치를 이해하게 함, 수학적 사고, 태도의 육성, 수학과목에 대한 불안심리불식, 수학적 사고의 종류와 여러 학자들의 견해, 수학적인 생각의 구조화, 발문분석과 실험수업 등을 학습한다.
Learning and establishing the cultivation of mathematical thoughts, the definition of specific contents and mathematical thoughts, the guidance for mathematical thoughts, the comprehension of the value of mathematical thoughts, we will study the cultivation of mathematical thought and attitude, the exclusion of anxiousness about math subject, the kinds of mathematical thoughts, several scholars’ opinions about them, the formation of mathematical thoughts, epilogue analysis and experimental classes.
MAE4033	수리논술	Discourse on Mathematics Principle
수학문제를 증명하고 사고를 논리적으로 명확하게 하기위해 논리에 대해 공부한다. 또한 논리적인 사고능력을 기르고 이를 바탕으로 많은 문제를 접함으로써 다른 수학 영역의 다양한 문제 해결과 정리, 증명의 방법을 습득하도록 한다.
It is one of the required courses to be a mathematical teacher of middle or high schools. In order to solve and prove mathematically problems, students must to learn logics. Also this course deals with various problems and many method solving that.
MAE4036	정수론	Number Theory
Division Algorithm과 Euclidean algorithm을 시작으로 Congruence, Fermat 정리, Euler phi-function, Euler 정리, Primitive Roots, Indices, Quadratic Reciprocity Law 등에 대하여 학습한다.
This course deals with Division Algorithm, Euclidean algorithm, congruence, Fermat’s theorem, Euler’s theorem, primitive roots, indices, and Quadratic Reciprocity Low.
MAE4037	확률 및 통계	Introductory Mathematical Statistics
이 과목에서는 확률변수, 분포함수, 큰 수의 법칙, 중심극한 정리, 다변량분포함수, 통계적 추정, 통계적 가설의 검정 등 기초확률론과 통계학 이론을 공부한다.
This course is for the studying the basic probability and statistics theory such as random variables, probability distribution functions, the law of large numbers, the central limit theorem, multi-variable distribution functions, statistical estimation and tests of statistical hypotheses.
MAE4038	복소해석학1	Complex Analysis 1
복소수의 성질과 기하적인 의미를 고찰하고 복소함수의 이론적 배경이나 정리들을 체계화하고, 응용부분도 다룬다. 아울러 고교수학에서 다루는 복소수와의 연계성도 알아본다.
This course teaches characteristics of complex numbers and geometric meaning, systematically guides through theoretical background and theory of complex variables, and shows how to apply. Futhermore, this course presents relations of complex numbers that you have learned in high school.
MAE4039	현대대수학1	Modern Algebra I
군에 관한 정의를 배우고, 군과 군위에서의 정의된 준동형사상, 동형사상에 대하여 공부한다. Sylow 정리, 자유가환군, 자유군에 대하여 학습한다.
In this course students learn the definition of homomorphism and isomorphism defined in group. Also, they study Sylow Theorem, free abelian groups, and free groups.
MAE4040	위상수학1	Topology I
중등학교 수학교사를 위한 교육과정의 하나로, 집합에도 대수가 있다는 것을 나타내고, 이어서 관계와 그의 시각화, 실수의 정체, 실수의 연속성 등을 다루며, 가깝다와 멀다라는 뜻이 성립할 수 있는 보다 추상화된 근접성의 개념인, 점의 개성을 고찰하는 방법, 위상공간, 그 외에 여려 가지 개념 및 거리공간, 거리공간의 일반화 및 추상화 등을 소개한다.
This course is one of curriculums for math teachers. Topological space shows that a set has algebra, and it deals with its relationship, visualization, accumulation of real number and continuity of real numbers. Also, it introduces a method to consider characteristics of points, which are concepts of more abstracted proximity that a meaning of far and close can be formed, topological space, other concepts, metric space, generalization and abstraction of metric space.
MAE4041	현대대수학2	Modern Algebra II
환은 연산이 덧셈, 곱셈의 두 연산위에 정의되며, 환의 연산 중에 곱셈연산에 조건을 하나씩 첨부시켜 가환군, 체 등을 정의하고 그 성질들을 살펴본다. 또 Galois이론에 대하여 공부한다.
This course teaches a ring with an additive operation and a multiplicative operation. It teaches a commutative ring and a field. Also, it studies Galois’s theory.
MAE4042	위상수학2	Topology II
일반적으로 한 위상공간 위에서 점열의 수렴성만을 가지고 어느 한 점에 가깝게 접근한다는 것을 완벽하게 나타낼 수 없다. 이에 수렴의 개념으로 네트와 필터가 필요로 한다. 또한 한 집합 위에 도입된 위상을 이용하여 부분집합들 사이의 분리된 정도를 나타내는 분리공리를 취급하며, 실직선 위에서 구간들이 갖는 기본 성질을 추상화하여 연결성의 개념 등을 취급한다.
Generally, there is no completely making a near approach to a certain point only with the pointwise convergence on the topological space. In the result, convergent net and filter are needed. Besides, by using the topology introduced on a set, this course deals with the separation axiom showing the proportion between subsets, and the concept of connectivity by abstracting the basic characteristics that the sections have on the real line.
MAE4043	복소해석학2	Complex Analysis 2
복소해석학Ⅰ을 이수한 후, 이를 바탕으로 복소변수함수에 대한 제반이론과 복소적분법, 복소적분을 이용한 실적분의 계산, 응용도 다룬다. 아울러 복소수, 복소평면, 복소수와 평면 벡터의 기하적인 해석 등을 고교수학에서 어떻게 지도할 것인가에 대한 연구도 한다.
After having completed complex variables l, on the base of it, this course deals with general theories on complex variables, complex integral calculus and the calculation and the application of real integral calculus, using complex calculus. Moreover, this course studies how to teach complex numbers, complex planes and the geometric analysis of complex numbers and plane vector in the field of middle or high school mathematics.
MAE4044	미분기하학	Differential Geometry
우선, 평면 혹은 공간 위에서 곡선을 어떻게 연구할 것인가, 그것들을 어떻게 해석적으로 연구할 것인가를 검토한다. 또한 역으로 평면 혹은 공간 위에서 곡선을 어떻게 정의할 수 있는가, 즉 곡선의 기하학적인 의미를 이해하는 데는 곡선이 어떤 방법으로 구부러지는가를 아는 것이라는 것을 배운다. 또한 곡면의 정의와 곡면을 형성하는 몇 가지 표준적인 방법에서 시작하여, 좌표조각사상, 미분가능함수와 곡면의 기본형식, 곡면에 대한 미분형식, 곡면의 사상 형식의 적분, 곡면의 위상적인 성질 등을 조사한다.
First of all, this course considers the way students should study curved lines on a plane or a space, and the way to do those in terms of analysis. On the contrary, students learn how to define a curved line on a plane or a space, that is, the way how a curved line can bend in what way, which explains the geometric meaning of a curved line. In addition, starting from the definition of a curved plane and several standard ways to form a curved plane, this course investigates coordinate patch, differential function and the basic form of curved plane, the differential calculus form of a curved plane, the integral calculus of coordinate patch of a curved plane and the topological characteristics of a curved plane.
MAE4045	수학교육론	General Theory of Mathematics Education
수학교육과 관련된 일반적인 지식을 학습하고, 수학교육의 다양한 이론을 탐구하고 논의함으로써 수학교육에서 발생하는 여러 문제를 해결할 수 있는 능력을 갖추게 한다.
This subject will help students to inquire and discuss on various theory of mathematics education, and to acquire general knowledge related mathematics education, in order to develop various problems solving ability occurred in mathematics education.
MAE4046	수학교재연구 및 지도법	Study of mathematics textbooks and teaching methods
예비교사로서 갖추어야할 가장 기본적인 수학교재에 대한 이해와 그 이해를 바탕으로 학생들을 직접지도할 수 있는 능력을 길러줄 수 있는 훈련과정의 기회를 제공한다.
This subject will provide an opportunity of training process that can help preservice teachers to increase teaching ability on the basis of understanding of mathematics textbooks.

개인정보처리방침

(04620) 서울특별시 중구 필동로 1길 30 동국대학교 수학교육과 (학림관(J동) 1층 105호) Tel : 02-2260-8749Fax : 02-2266-3409